Hierarchical Clustering

hierarchical clustering은 각 data point를 하나의 클러스터로 간주하고 반복적으로 가장 가까운 두개의 클러스터를 합쳐나가는 방식이다.
hierarchical clustering은 single cluster에서 시작하여 가까운 cluster를 반복적으로 합쳐나가는 상향식 방법인 Agglomerative approach와 all inclusive한 cluster에서 쪼개나가는 하향식 방식인 Divisive approach로 나누어진다. Divisive approach의 경우 어떠한 기준으로 split하는지의 경우를 고려하는 비용이 크므로 잘 사용하지 않고, 이번 포스팅에서는 Agglomerative에 대해서만 설명하고자 한다.
Agglomerative Hierarchical Clustering

* Basic Algorithm
| 1 : Make each point as a singleton cluster 2: repeat 3: Merge the closest two clusters 4: until only one cluster remains |
Three important questions
클러스터링은 가장 가까운 두 개의 클러스터를 합쳐나가는 방식이므로 두 점 사이의 거리를 구하기 위해서는 거리를 구할 두 점이 필요하다. 두 클러스터 안에 원소가 각각 하나만 있다면 클러스터 사이의 거리를 구하는 것은 어렵지 않지만 cluster가 여러 개의 data point로 이루어진 경우 1) 어떤 point가 클러스터를 대표하며 2) 두 점간의 거리를 어떻게 정의할 것인지에 대한 문제가 발생하게 된다. 또한 수많은 점들을 클러스터링 해나갈 때 3) 어느 시점까지 클러스터링을 할 것인지에 대한 문제가 발생한다.
Q1. Cluster Representative
In the Euclidean case
유클리드 공간의 경우에는 각 클러스터는 데이터포인트들의 평균값인 centroid를 가진다.
예를 들어, 각 좌표가 (1, 1), (2, 2), (3, 0) 이라면 centroid는 (2, 1)이 된다.
이제 유클리드 공간에서는 두 클러스터 사이의 거리는 두 centroid 사이의 거리로 정의할 수 있다.
In the Non-Euclidean case
반면 유클리드 공간이 아닌 경우에는 데이터 포인트간의 거리 개념을 사용할 수 없다.
예를 들어 두 문서의 유사도를 측정하는 경우에는 거리 개념을 사용할 수 없다.
이를 해결하기 위해 cluster내의 다른 point간 가장 가까운 point인 clustroid를 사용한다.
좋은 clustroid를 선택하기 위해서 아래와 같은 여러 방법이 존재한다.
1) 다른 점들과의 최대거리를 최소화하는 점을 선택
2) 다른 점들간의 거리의 합을 최소화하는 점 선택
3) 다른 점들과의 거리의 제곱합을 최소화 하는 점을 선택
example

eidt distance를 사용하고, abcd, aecdb, abecb, ecdab라는 4개의 점을 가지고 있다고 가정해보자.
각 점들간의 edit distance를 구해야하는데 abcd와 ecdab의 거리 하나만 여기서 구해보자!
edit distance = 4 + 5 - 2*2 = 3
모든 점에 대한 edit distance를 구한 후 sum - sq를 최소화하는 점을 clustroid로 정한다.
* Edit distance
Edit distance는 두 문자열 데이터간의 거리로, insertion과 deletion을 최소화하는 거리를 의미한다.
예를 들어 x = abcde , y = acfdeg라고 하면 edit distance는 3이 된다.
1) b를 삭제 → 2) f를 c뒤에 넣음 → 3) e뒤에 g를 넣음
하지만 이러한 방식은 문자열이 길어질 수록 적합하지 않기 떄문에, LCS(Longest Common Subsequence)를 사용한다.
edit distance = ||x|| + ||y|| - 2||LCS||
LCS = 왼쪽에서 오른쪽으로 순서대로 가장 긴 sequence의 길이 ( 반드시 연속적일 필요 X )
위의 예시를 다시 살펴보면 ( x = abcde , y = acfdeg )
||x|| = 5 , ||y|| = 6 , ||LCS|| = 4 이므로
edit distance = 5 + 6 -2*4 = 3

위 사진을 보면 centroid는 클러스터 내의 모든 점들의 평균으로 인위적으로 만든 점이다.
반면 clusteroid는 클러스터 내의 모든 다른 점과 가까운 클러스터내의 존재하는 점이라고 보면 된다.
Efficiency
시간복잡도를 구하기 위해 클러스터링을 하기 위한 원소의 개수를 N개라고 하자.
모든 클러스터간의 거리를 계산해야해야 하므로O(N^2)의 시간이 걸리고,
그것들을 모두 합칠 때 N^2 + (N-1)^2 + (N-2)^2 + ... + 1 이므로, 결국 O(N^3)의 시간이 걸린다.
조금 효율적인 방법은 우선 순위 큐(priority queue)를 사용하는 방법이 있는데 이는 O(N^2 log N)까지 시간 복잡도가 감소한다. 모든 점과 점 사이의 거리를 우선 순위 큐에 넣을 때 O(N2logN) 시간이 소요되고, 클러스터를 합칠 때, 클러스터를 합침으로써 영향을 받는 거리들만 다시 계산할 때 O(N)이 소요되므로 이 방법의 시간복잡도는 logN)이 된다. 하지만 이 방식도 빅데이터셋에는 여전히 비효율적인 방법이다.
Q2. Defining Nearness of Clusters
클러스터간의 거리를 구할 때 클러스터 안의 점은 여러 개가 존재하므로 두 점간의 거리를 정의내리는 것이 중요하며, 통상적으로 아래와 같은 방식을 사용한다.
* Proximity between Clusters
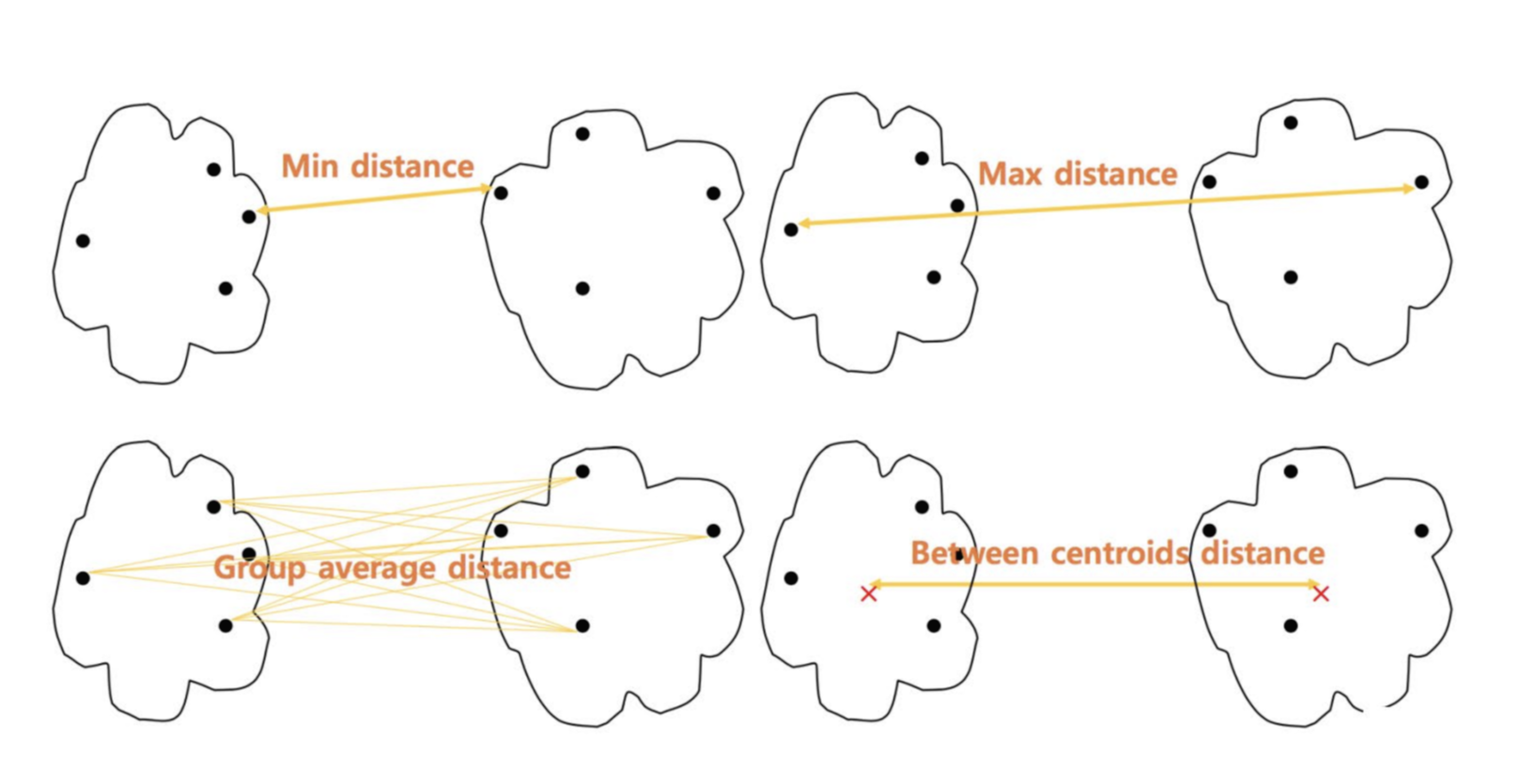
1) MIN
- distance between the closest two points in different clusters
- 서로 다른 클러스터에서 두 데이터포인트 사이의 가장 가까운 거리
- 이 직선보다 짧은 직선은 존재하지 않으므로 single link라고 한다
- MIN의 경우 바로 옆에 있는 데이터포인트를 즉시 clustering하여 키워나가므로 옆으로 길쭉해지는 모양이 나오는 경우가 다수
- 타원형(no-elliptical)의 경우 클러스터링이 용이하나, outliers에 sensitive하다
2) MAX
- distance between the farthest two points in different clusters
- 서로 다른 클러스터에서 두 데이터포인 사이의 가장 먼 거리
- 가장 긴 직선보다 짧은 점들을 이으면 모든 직선이 포함되므로 complete link라고 한다
- outlier에 취약하진 않으나, 원형(globular)의 클러스터링에만 용이하다
- 타원형의 데이터 모양에 MAX를 사용하면 k-means와 비슷한 결과가 나오게 된다
3) Group average distance
- average distance of all pairs of points
- MIN과 MAX을 합친 방식
4) Centroid distance
- cetroid간의 거리
5) Ward's Method
- 두 클러스터를 합쳐졌을 때 SSE가 얼마나 증가했느냐를 distance로 결정함 (점들간의 거리 개념이 아님!)
- SSE : 새로운 클러스터가 형성되면 그 클러스터의 centroid와 cluster내의 점들 간의 거리의 제곱합
- SSE를 최소로 하는 cluster를 merge
- K-means과 비슷한 결과를 가지나, 계산비용이 많이 든다
- outlier와 noise에 가장 효과적인 방법
'Data Mining' 카테고리의 다른 글
| DBSCAN (밀도 기반 클러스터링) (0) | 2021.11.22 |
|---|---|
| K-means Clustering (K-평균 군집화) (0) | 2021.11.22 |
| Clustering (군집화) (0) | 2021.11.20 |
| Flajolet-Martin Algorithm (0) | 2021.11.10 |
| Bloom filters (0) | 2021.11.06 |



댓글