DBSCAN

DBSCAN은 밀도 기반의 클러스터링 알고리즘입니다. 같은 클래스에 속하는 데이터는 서로 근접하게 분포할 것이다'라는 가정으로 시작하며, 밀도 기반으로 클러스터링하기 때문에 데이터셋이 불특정한 분포를 가질 때 유용합니다.
Density
밀도(Density)는 한 데이터포인트의 Eps(거리반경)내에 있는 포인트의 수를 의미합니다. 간단히 말하면 Eps 내에 데이터가 몇 개 있는가?라고 생각하면 되는데, 이때 Eps는 자기 자신의 점을 포함한 반경을 의미합니다.
결국, 각 포인트의 밀도는 Eps를 어떻게 설정하느냐에 따라 달라지게 됩니다. 만약 eps가 너무 크면 모든 점들이 반경 안에 포함되기 때문에 비슷한 밀도를 가지게 되고, eps가 너무 작으면 모든 포인트들이 자신 뺴고 그 반경에 속하지 않으므로 밀도는 1이 되게 됩니다.
Points

DBSCAN에서 각 데이터 포인트는 3개의 포인트 중 하나로 분류될 수 있습니다.
1) Core points
core point는 밀도가 높은 핵심(내부)를 구성하는데, Eps 내에 최소 N개의 데이터(Minpts)가 있어야 core point라 할 수 있습니다. 결국 Eps와 Minpts는 사용자게 제공해야하는 파라미터입니다. 위의 예에서 Minpts를 7로 잡았다면 점 A는 자기 자신을 포함하여 eps 내에 7개의 데이터를 가지고 있기 때문에 core point라 할 수 있습니다.
2) Border points
Border point는 밀도는 높지 않으나 근처에 core point가 존재하여 cluster의 가장자리에 위치하는 데이터입니다. 아까와 마찬가지로 Minpts가 7이라고 가정한다면 점 B는 Minpts가 4이지만 eps 내에 core point가 존재하기 때문에 border point로 분류됩니다.
3) Noise points
noise point는 eps내의 Minpts도 충족하지 않고, core point도 없는 경우에 분류될 수 있습니다.
DBSCAN Algorithm

DBSCAN 알고리즘의 기본적인 동작은 다음과 같습니다.
1) 모든 data points를 3개의 포인트로 분류한다
2) noise point는 버린다
3) Eps내의 core point 끼리 엣지로 연결 → 연결된 포인트를 모아 클러스터를 형성
4) border point는 자신의 반경 내의 core point들 중 하나의 core point가 속한 클러스터에 할당한다
Parameters

Eps와 MinPts는 사용자가 제공해야하는 파라미터라고 했는데, 이 때 k번째로 가까운 이웃간의 거리인 K-dist를 이용합니다.
같은 클러스터에 포인트들이 많으면 k-dist 값은 작아지고, 클러스터 내에 포인트가 적으면 k-dist값은 커집니다.
모든 점에 대해 k-dist를 구한 후, k-dist를 오름차순으로 정렬합니다. (e.g., k = 5)
그 후 k-dist가 급격하게 증가하는 부분을 끊어, 그 구간을 Eps로 설정합니다. (eps = 0.15)
위의 사진을 보면 대략 5000개의 점들은 K-dist가 0.15보다 작습니다. 그렇기 때문에 대부분의 점들은 반경 0.15 안에 최소 5개 의 점이 존재한다고 말할 수 있습니다. 결론적으로 k-dist가 eps보다 작으면 그 포인트는 코어 포인트로 분류할 수 있고, 나머지 포인트들은 noise point나 border point로 분류되게 됩니다.
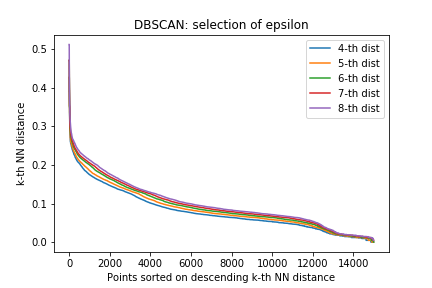
결국 Eps의 값은 K-dist의 K값에 달려있습니다. 하지만 K값은 급격하게 변하지 않기 때문에 보통 DBSCAN 알고리즘의 경우 k를 4로 설정합니다. 2차원의 데이터셋에서는 k가 4와 8 사이라면 거의 비슷한 양상을 보이기 때문에 사실상 k를 어떤 것으로 선택하든 상관이 없습니다.
Clusters of Varying Density

DBSCAN의 경우 클러스터들의 밀도가 변함에 따라 문제가 발생합니다. 예를 들어, 클러스터 C와 D를 찾기위해서 MinPts를 7로 설정했다고 가정해보겠습니다. 그렇다면 왼쪽의 경우에는 모든 포인트가 core point가 되어 대형의 single 클러스터를 형성하게 됩니다.
하지만, MinPts를 9로 설정하게 된다면, 오른쪽의 경우 모든 포인트가 noise point가 됩니다. 그래서 구역마다 밀도가 다른 것은 반영하지 못한다는 단점을 가집니다.
Strength and Weeknesses
장점
- 노이즈를 자동으로 제거하기 때문에 노이즈에 강하다
- 원형이 아닌 임의의 모양으로 클러스터링이 가능하다. 즉, k-means가 찾지 못하는 클러스터링이 가능!
- k-means처럼 클러스터의 개수를 정하지 않아도 된다.
단점
- 지역데 따른 상대적인 밀도 반영이 어렵다
- k-dist를 모든 점에 대해 구해야하므로 계산 비용이 크다.
- 고차원으로 갈수록 모든 점의 거리가 비슷하게 다 멀어지므로 거리 자체에 의미가 사라지게 되어 밀도를 구하기 어려워진다.
참고 )
K-means Clustering (K-평균 군집화)
K-means Clustering K-means에서 K는 클러스터의 개수를 의미하고 means는 평균을 의미한다. 말 그대로 주어진 데이터를 k개의 클러스터로 묶는 알고리즘이다. Basic Algorithm 1: Select K points as initial c..
minutemaid.tistory.com
'Data Mining' 카테고리의 다른 글
| CURE Algorithm (Clustering Using REpresentatives) (0) | 2021.11.22 |
|---|---|
| BFR Algorithm (0) | 2021.11.22 |
| K-means Clustering (K-평균 군집화) (0) | 2021.11.22 |
| Hierarchical Clustering (계층적 군집) (0) | 2021.11.22 |
| Clustering (군집화) (0) | 2021.11.20 |




댓글